Otros aspectos de la Cinemática de los sólidos.

Centro de gravedad.

El centro de gravedad o centro de masas de un sistema continuo es el punto geométrico.

En mecánica del sólido rígido, el centro de masa se usa porque tomando un sistema de coordenadas centrado en él, la energía cinética total K puede expresarse como  , siendo M la masa total del cuerpo, V la velocidad de traslación del centro de masas y Krot la energía de rotación del cuerpo, expresable en términos de la velocidad angular y el tensor de inercia.

Velocidad angular.

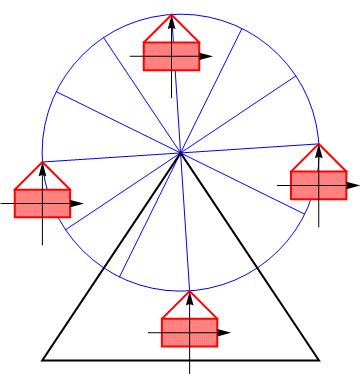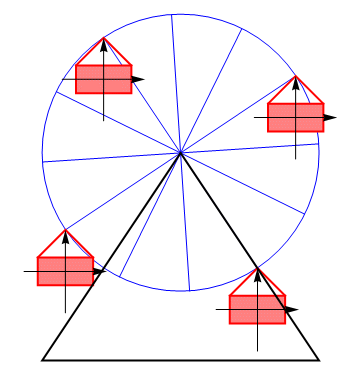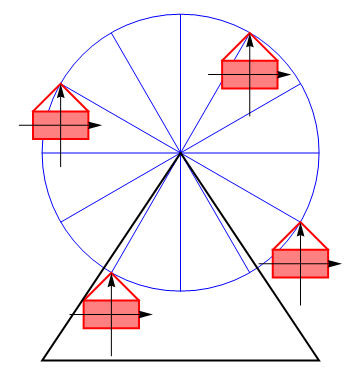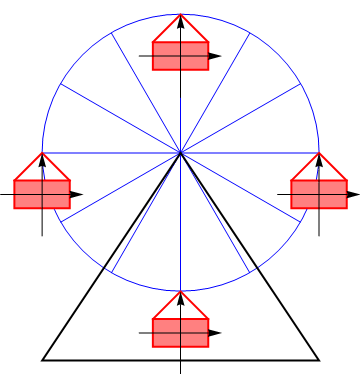
Sea una partícula cualquiera de un sólido rígido el cual se desplaza girando. Dado que todos los puntos están rígidamente conectados podemos hacer la siguiente descomposición de posición y velocidades, tomando un punto de referencia arbitrario.


Momento angular o cinético.

Artículo principal: Momento angular.
El momento angular es una magnitud física importante porque en muchos sistemas físicos constituye una magnitud conservada, a la cual bajo ciertas condiciones sobre las fuerzas es posible asociarle una ley de conservación. El hecho de que el momento angular sea bajo ciertas circunstancias una magnitud cuyo valor permanece constante puede ser aprovechado en la resolución de las ecuaciones de movimiento. En un instante dado, y fijado un punto del espacio en un punto del espacio O.


Espacio de configuración de un sólido rígido.

La mecánica lagrangiana para describir un sistema mecánico con un grado finito de grados de libertad se define como una variedad diferenciable llamada espacio de configuración. El movimiento del sistema o evolución con el tiempo se describe como un conjunto de trayectorias a lo largo del espacio de configuración. Para un sólido rígido con un punto inmóvil (sólo existe rotación) el espacio de configuración viene dado por la variedad diferenciable del grupo de rotación SO(3). Cuando el sólido tiene traslación y rotación de todos sus puntos el espacio de configuración es E+(n), el subgrupo de isometría del grupo euclídeo (combinaciones de traslaciones y rotaciones.

Tensor de inercia.


Cuando se estudia el movimiento de un sólido rígido resulta conveniente descomponerlo en un movimiento de traslación más un movimiento de rotación:
Para describir la traslación sólo necesitamos calcular las fuerzas resultantes y aplicar las leyes de Newton como si se tratara de puntos materiales.
En cambio la descripción de la rotación es más compleja, ya que necesitamos alguna magnitud que de cuenta de como está distribuida la masa alrededor de cierto punto o eje de rotación (por ejemplo un eje que pase por el centro de masa). Esa magnitud es el tensor de inercia que caracteriza la inercia rotacional del sólido.
Ese tensor de inercia sólido rígido se define como un tensor simétrico de segundo orden tal que la forma cuadrática construida a partir del tensor y la velocidad angular ω da la energía cinética de rotación,

Mecánica de un solido rígido.

La mecánica de un sólido rígido es aquella que estudia el movimiento y equilibrio de sólidos materiales ignorando sus deformaciones. Se trata, por tanto, de un modelo matemático útil para estudiar una parte de la mecánica de sólidos, ya que todos los sólidos reales son deformables. Se entiende por sólido rígido un conjunto de puntos del espacio que se mueven de tal manera que no se alteran las distancias entre ellos, sea cual sea la fuerza actuante (matemáticamente, el movimiento de un sólido rígido viene dado por un grupo uniparamétrico de isometrías).

                             

Movimiento Rototraslatorio.

El movimiento más general del sólido rígido es el movimiento rototraslatorio; esto es, el originado por la superposición de los dos movimientos básicos: el movimiento de traslación y el movimiento de rotación.
Consideremos un sólido rígido que está animado simultáneamente de un cierto número de movimientos de traslación y de rotación. Cada uno de los movimientos de traslación quedará completamente definido por la velocidad de traslación correspondiente; esto es, v1, v2, ... vm. Análogamente, cada una de las rotaciones quedará completamente definida por el vector velocidad angular correspondiente; esto es ω1, ω2, ... ωn. Teniendo en cuenta que un movimiento de traslación es equivalente a un par de rotaciones cuyo momento es igual a la velocidad de traslación, el estado de movimiento del sólido rígido estará definido por un conjunto de rotaciones simultáneas, ω1, ω2, ... ωn, ωn+1, ... ωn+2m, cuyos ejes de rotación pasan por los puntos O1, O2, ... On+2m .

La velocidad de un punto genérico del sólido, P, viene dada por el momento resultante del sistema de vectores deslizantes ωi (i=1, 2, ...) en el punto P; i.e.



Por otra parte, el momento del sistema de vectores deslizantes en otro punto, P′, del sólido (i.e., la velocidad del punto P′) está relacionado con el anterior mediante la expresión.




siendo ω = Σωi la resultante general del sistema de vectores deslizantes (i.e., la velocidad angular resultante) que es un invariante del sistema (primer invariante o invariante vectorial).
La expresión [33] nos permite decir que la velocidad que le corresponde a un punto P′ de un sólido rígido es igual a la que le corresponde a otro punto arbitrario del mismo, P, más la velocidad que le correspondería al punto P′ en una rotación instantánea, ω, alrededor de un eje que pasase por el punto P. En definitiva, podemos enunciar:
El movimiento general de un sólido rígido (movimiento rototraslatorio) puede reducirse a una rotación de velocidad angular ω = Σωi alrededor de un eje paralelo a ω y que pasa por un punto arbitrario del sólido, más una traslación cuya velocidad es el momento resultante del sistema de vectores ωi (i=1, 2,...) con respecto a dicho punto arbitrario.
El enunciado anterior nos indica que cualquier movimiento del sólido rígido, por complejo que nos parezca, puede reducirse siempre a la superposición de dos movimientos básicos: uno de traslación y otro de rotación. Obsérvese que la velocidad de cualquier punto del sólido queda perfectamente determinada con el conocimiento de la velocidad angular ω del sólido y la velocidad vP de un punto cualquiera del mismo; i.e., por los vectores ω y vP, a los que denominaremos, conjuntamente, grupo cinemático en P.

Movimiento de rotación.

Propiedades generales.

Supongamos ahora que:




de forma que la velocidad instantánea de cada punto se reduce a



Esta forma del campo de velocidades posee una serie de propiedades que lo identifican como movimiento de rotación:

La velocidad del punto O es nula  

Todos los puntos situados en la recta que pasa por O y tiene la dirección de    poseen velocidad nula:



Esta línea se conoce como eje instantáneo de rotación (EIR).



Alternativamente, el movimiento de rotación se puede caracterizar a partir del estado de dos puntos cuya velocidad es nula y un tercero, P, no colineal con ellos, con velocidad no nula, . En ese caso el resto del campo de velocidades es el de una rotación pura con eje el que pasa por los dos primeros puntos y con velocidad angular de módulo vP / d siendo d la distancia de P a la recta que pasa por los otros dos.

Al estudiar el movimiento de rotación y describir las velocidades según la ley se puede adquirir la idea errónea de que las partículas del sólido describe un movimiento circular. Eso NO es correcto. Lo que hemos hecho es describir la distribución instantánea de velocidades, esto es, qué velocidad tiene cada punto del sólido en un instante dado, pero no hemos analizado cómo se mueve cada punto a lo largo del tiempo (en términos llanos, hemos tomado una fotografía, no una película de vídeo).




Consideremos el caso de un cilindro que rueda sobre el suelo. La línea de contacto esta formada por puntos con velocidad nula y por tanto se trata de un eje instantáneo de rotación. El cilindro está efectuando una rotación pura instantánea en torno a esta línea de contacto (y no respecto al eje del cilindro, como podría pensarse), pero la trayectoria de cada punto del cilindro no es una circunferencia, sino una cicloide (técnicamente, para los puntos que no son de la superficie exterior es una cicloide acortada).

La razón es que aunque instantáneamente esté rotando en torno a esta línea, el eje de rotación va cambiando en el tiempo.

Movimiento de traslación.

El movimiento de traslación es el más sencillo que puede realizar el sólido rígido. Desde un punto de vista geométrico, lo podemos definir del modo siguiente.

Se dice que un sólido rígido se encuentra animado de un movimiento de traslación cuando todo segmento rectilíneo definido por dos puntos de aquél permanece paralelo a si mismo en el transcurso del movimiento.
Consideremos un sólido rígido animado de un movimiento de traslación. En virtud de la condición geométrica de rigidez, el vector rij = ri-rj debe mantener constante su módulo en el transcurso de cualquier movimiento y, además, en virtud de la definición geométrica del movimiento de traslación, también ha de mantener constante su dirección; entonces, siendo c un vector constante, se puede escribir:




y derivando con respecto al tiempo



constituyendo esta igualdad la condición cinemática del movimiento de traslación, esto es:


Todos los puntos de un sólido rígido animado de un movimiento de traslación tienen, en cada instante, la misma velocidad.

Esa velocidad, común a todos los puntos del sólido, recibe el nombre de velocidad de traslación del sólido y debe ser considerada como un vector libre. Las mismas consideraciones pueden aplicarse a la aceleración. En consecuencia, una vez definido el movimiento de un punto cualquiera del sólido rígido que se traslada, tenemos definido el movimiento del sólido.

Otra característica importante del movimiento de traslación del sólido rígido es que las trayectorias recorridas por sus diversos puntos son congruentes, es decir, una se puede obtener mediante una translación de la otra. En efecto, consideremos de nuevo dos puntos cualesquiera, Pi y Pj, pertenecientes al sólido, y sean ri y rj sus vectores de posición con respecto a un cierto origen arbitrario O. Imaginemos un desplazamiento experimentado en una traslación del sólido, de modo que los vectores de posición de esos puntos, con respecto al mismo origen O, sean ahora r′i y r′j, respectivamente. La condición geométrica de rigidez junto con la condición geométrica que define al movimiento de traslación, se expresa en la forma




de modo que el desplazamiento experimentado por cada uno de los puntos del sólido durante un intervalo de tiempo Δt es único. De este resultado, junto con la noción de la línea curva como límite de una poligonal y de la continuidad del movimiento, se sigue la congruencia de las trayectorias recorridas por los distintos puntos del sólido rígido.
Es conveniente que insistamos en que el movimiento de traslación no prejuzga forma alguna para las trayectorias de los distintos puntos que constituyen el sólido. Evidentemente, si la velocidad de traslación es constante (v=cte), cada uno de los puntos del sólido recorrerá una trayectoria rectilínea con celeridad constante y todas esas trayectorias serán paralelas entre sí (movimiento de traslación uniforme). Pero, en general, la velocidad de traslación no tiene por que ser constante y la trayectoria puede ser curvilínea. Así, por ejemplo, las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la Figura; la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectoria circular.

                                         

                            

Estado de reposo.

El caso más simple de estado de movimiento es el que tiene

        

En este caso todos los puntos del sólido se encuentran en reposo:



Equivalentemente, este estado se puede enunciar diciendo que si tres puntos no colineales de un sólido se encuentran en reposo, entonces todos los demás también están en reposo.

El estado de reposo puede ser

Instantáneo.

Si la velocidad de todos los puntos se anula en un momento dado, para al instante siguiente dejar de ser nula.

Permanente.

Si este estado se mantiene durante un cierto intervalo de tiempo.

Campo de velocidades.

Cuando un sólido se mueve, cada uno de sus puntos lo hará, en principio, con una velocidad diferente. Tenemos entonces que la distribución de velocidades forma un campo vectorial.




La velocidad de cada punto es un vector ligado a dicho punto y por tanto carece de sentido hablar de la “velocidad de un sólido”, como si fuera algo único. Podremos hablar de la velocidad de un punto del sólido, o, en su caso, de la velocidad de su centro de masas, pero no de la velocidad del sólido como un todo.

De acuerdo con el modelo de sólido ideal, podemos suponer esta distribución de velocidades como extendida a todo el espacio. En un sólido real  ,  solo tendrá significado en aquellos puntos en que haya partículas materiales.

La condición de rigidez impone limitaciones a las posibles distribuciones de velocidades. Solo aquellos movimientos que preservan las distancias entre los puntos son admisibles. Estos movimientos posibles se conocen como movimientos rígidos.

Puede demostrarse que la forma más general del campo de velocidades de un sólido (según el Teorema de Chasles) es:




siendo   y   dos vectores independientes de la posición (pero no del tiempo, no son constantes en general). Aquí    es la posición respecto a un cierto punto O que tomamos como origen de coordenadas.

Si etiquetamos la posición del origen por O y la de un punto cualquiera por P, la forma general del campo de velocidades puede escribirse como  

Condición de rigidez.

 Condición geométrica.

Matemáticamente, un sólido rígido se caracteriza por ser un sistema de partículas tal que la distancia entre cada par de partículas que lo componen permanece constante en cada momento.




Esta es la condición geométrica de rigidez. Si empleamos letras para indicar las posiciones de cada partícula, esta condición se expresa.




Puesto que se aplica a cada par de partículas supone N(N − 1) / 2 vínculos geométricos (tantos como el número de pares de partículas), si bien muchos de ellos son redundantes en cuanto a que son consecuencia unos de otros.

Condición cinemática.

Cada vínculo geométrico lleva asociado un vínculo cinemático, que establece una relación entre las velocidades posibles. Obtenemos estos vínculos derivando en la expresión de los vínculos geométricos.

Elevando al cuadrado




y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades.



Esta es la condición cinemática de rigidez, que podemos escribir



o, empleando letras, para cada par de puntos del sólido




Dividiendo por la distancia entre las partículas A y B




siendo cada miembro la proyección de la velocidad en la dirección del vector 




La condición cinemática de rigidez implica que, dadas dos partículas, A y B, la proyección de sus respectivas velocidades sobre la recta que las une es la misma. Por ello se dice que el campo de velocidades es equiproyectivo.


El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa.

Otra forma de verlo es considerar que  es la velocidad de la partícula B respecto a la A




y por tanto




nos dice que la velocidad relativa de una partícula respecto a otra o es nula o es perpendicular a la recta que las une. Si nos montamos en una partícula del sólido y desde allí observamos a otra partícula cualquiera del mismo sólido, veremos que la otra partícula ni se acerca ni se aleja: o se mantiene en reposo o gira alrededor de nosotros moviéndose sobre una superficie esférica en cuyo centro nos hallamos.

Cinemática de un solido rígido.

Compresibilidad nula.

Una vez descrito el sistema más sencillo, formado por una sola partícula, podemos pasar a sistemas más complejos, considerándolos formados por un agregado de partículas interactuantes.

Existen toda una serie de leyes generales y teoremas de conservación para sistemas de partículas, pero aquí nos centraremos en un agregado muy concreto, que es el modelo denominado sólido rígido.

Los sistemas macroscópicos suelen clasificarse en diferentes estados de la materia: sólidos, líquidos, gases y plasmas. De estos, los tres últimos se agrupan conjuntamente en el concepto de fluidos, por oposición a los sólidos.
La diferencia entre un fluido y un sólido es que mientras el fluido se adapta a la forma del recipiente que lo contiene, el sólido no lo hace. También se distinguen en su comportamiento cuando se ejerce una fuerza tangente a su superficie (fuerza de cizalla). Un fluido adquiere una velocidad en la dirección de la fuerza (velocidad dependiente de la viscosidad del fluido), mientras que un sólido se deforma en dicha dirección.

Todos los sólidos son deformables cuando se aplica una fuerza sobre ellos, y el grado con que lo hacen se mide por su elasticidad. En el caso de un resorte, esta deformabilidad se mide con la constante de recuperación que aparece en la ley de Hooke.

Cuanto menor es la compresibilidad de un sólido (o mayor su constante de recuperación) más indeformable es, más fuerza es necesaria para conseguir una dilatación dada. Por ejemplo, de acuerdo con la ley de Hooke, la dilatación de un resorte viene dada por





cuando K  la deformación tiende a cero, sea cual sea la fuerza aplicada.

Un primer estudio de los sólidos consiste, por tanto, en hacer el modelo de sólido completamente indeformable, o sólido rígido.

Extensión indefinida.

Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales.

Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a todo el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad.

Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido.

Debemos definir Cinemática y Cinemática de un solido rígido.

La cinemática (del griego κινεω, kineo, movimiento) es una rama de la física que estudia las leyes del movimiento (cambios de posición) de los cuerpos, sin tomar en cuenta las causas (fuerzas) que lo producen, limitándose esencialmente, al estudio de la trayectoria en función del tiempo. La aceleración es el ritmo con que cambia su rapidez (módulo de la velocidad). La rapidez y la aceleración son las dos principales cantidades que describen cómo cambia su posición en función del tiempo. La cinemática del sólido rígido es una aplicación de la cinemática al movimiento de un objeto tridimensional rígido en el espacio. El movimiento más general del sólido rígido puede considerarse como la superposición de dos tipos de movimiento básicos: de traslación y de rotación. Entendemos por sólido rígido un sistema físico en el que la distancia entre dos puntos materiales cualesquiera de ellas permanece invariable en el transcurso del tiempo. Los cuerpos sólidos que manejamos se deforman siempre, en mayor o menor grado, cuando están sometidos a las acciones de las fuerzas; sin embargo, si éstas son suficientemente pequeñas, las deformaciones producidas son despreciables y, entonces, hablaremos de cuerpos rígidos o indeformables. La definición de sólido rígido es sólo conceptual, por cuanto que el sólido rígido, en todo rigor, no existe. En este sentido, el sólido rígido es sólo una idealización y extrapolación del sólido real, al igual que lo es la partícula o punto material.